I write a lot of software in my spare time, a small portion of which will be posted here. Only those projects that I find most interesting will be posted. Note that I make no effort to ensure that this software will compile on any platform other than my own. The software below will be dependent only on the Boost libraries (most of which are on the standards track for C++), unless otherwise stated.
DISCLAIMER: I spend no time what-so-ever attempting to get this code to compile on varying platforms. It may not work on your platform “out of the box”.
Maze
This code generates a perfect maze, and then solves it. A perfect maze is defined as a maze which has one and only one path from any point in the maze to any other point. The maze and its solution are written out to a PNG file. This code makes use of C++11 constructs, so a relatively modern compiler will be required. Also note that this code depends on libpng.
Atomic Lock vs. std::mutex
Which is faster? For a quick discussion, click here. The source code is here.
Fractal
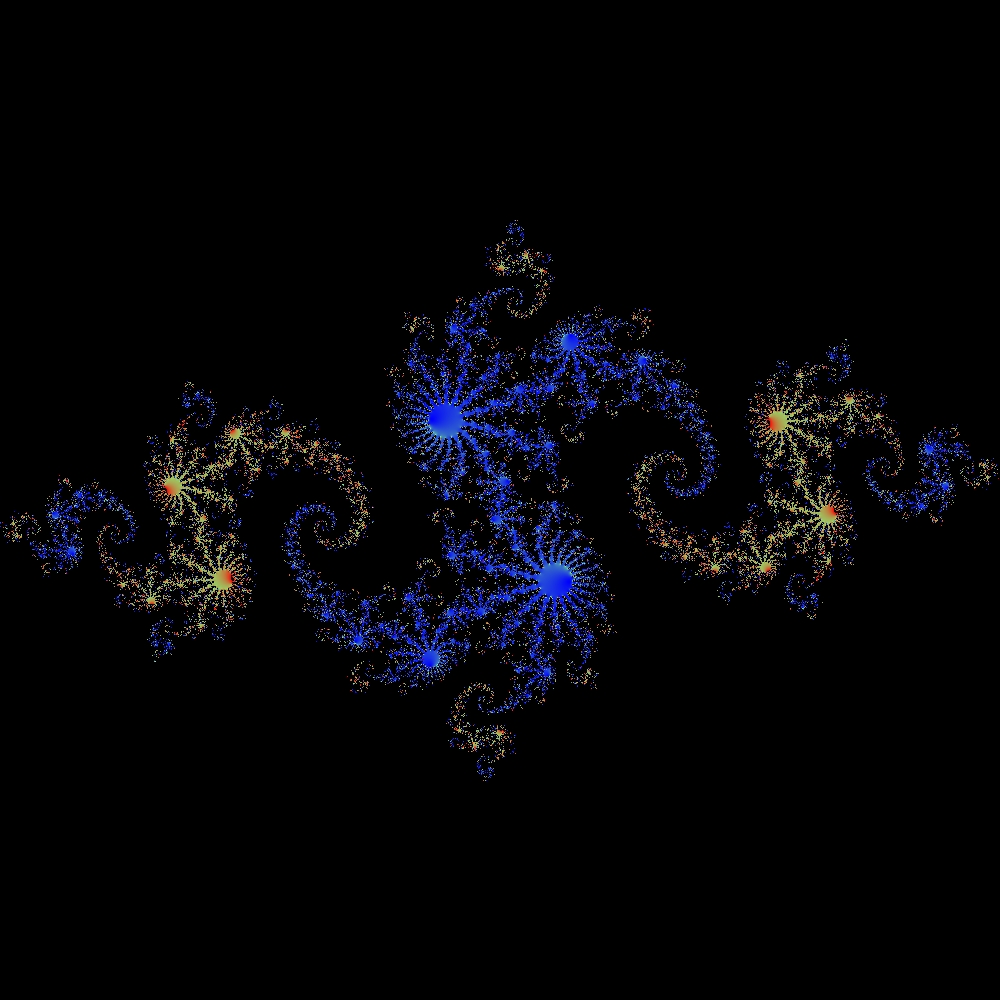
This software uses Newton’s method (the one from any first year calculus course) in the complex plane to generate fractals. This code makes use of many of the new C++11 language features, so a newer compiler will be required (I used GCC 4.8.1 running on Opensuse). This code is documented thoroughly with doxygen.
How it Works
A rectangular region is first chosen in the complex plane. Then, the fractal is computed row by row (a row is a line with all points on the line having a constant imaginary component – a horizontal line). Each point on the row is used as the initial guess for Newton’s method. Newton’s method will eventually converge on one of the zeros of the fractal generating function. The color of the associated pixel is chosen by which zero Newton’s method finds. The shading is derived from the number of iterations needed to reach the zero.
Source and Documentation
Throughput
This software models the throughput of a single queue with multiple producer and consumer threads. As the number of producer and consumer threads are varied (independently), performance is measured and recorded. The threads themselves execute both work and I/O, based on normal (or gaussian) distributions (that is, on each iteration, each thread is given an amount of work and I/O to perform, with the acutal amounts coming from a normally distributed random variable). The parameters of all distributions are controllable via a configuration file. The results of the test are then sent to GNU plot, for a graphical view. This program outputs a detailed profile file, that shows exactly where each thread spent its time. Obviously, this software depends on GNU plot (and, as stated above, Boost). It is very interesting to see the differences in throughput when this code is executed on a multi-core vs. a single core processor. Finally, thanks to the boost library, the same code executes on both windows and FreeBSD. The tarballs below contain identical code, but makefiles specific to the platform. The tarballs also contain a configuration file, and three output files.
Lock Free Queue
This software illustrates a queue that is thread safe, but uses no mutexes, semaphores, or other traditional methods to guarantee data integrity. Rather, this queue uses atomic operations to effect both enqueues and dequeues. This queue, therefore, never blocks either the enqueuing thread or the dequeueing thread. Because atomic operations are O/S dependent, this software will only compile on a single operating system, FreeBSD. Still the code is small and it works. It is a great example of how to do this sort of programming. This software does not depend on the boost libraries.