Maze
This code is just for fun. It generates a ‘perfect’ maze and solves it. The results are written out to a PNG file. For details, click here.
This code is just for fun. It generates a ‘perfect’ maze and solves it. The results are written out to a PNG file. For details, click here.
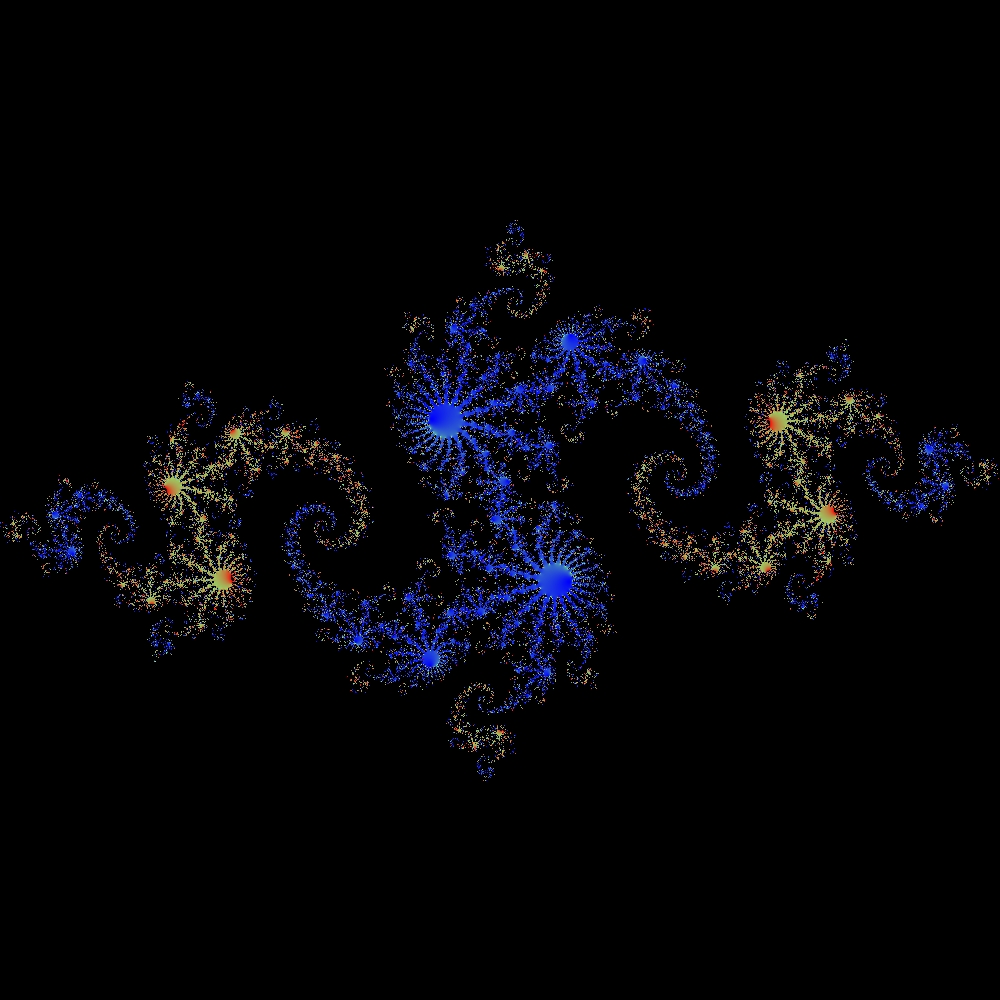
This software uses Newton’s method (the one from any first year calculus course) in the complex plane to generate fractals. This code makes use of many of the new C++11 language features, so a newer compiler will be required (I used GCC 4.8.1 running on Opensuse). This code is documented …
The Question Which is faster, a queue guarded by a std::mutex, or the same queue guarded by an atomic? This experiment attempts to at least partially answer that question. To do this, I constructed a queue that could be guarded by either a std::mutex or by my own atomic based …