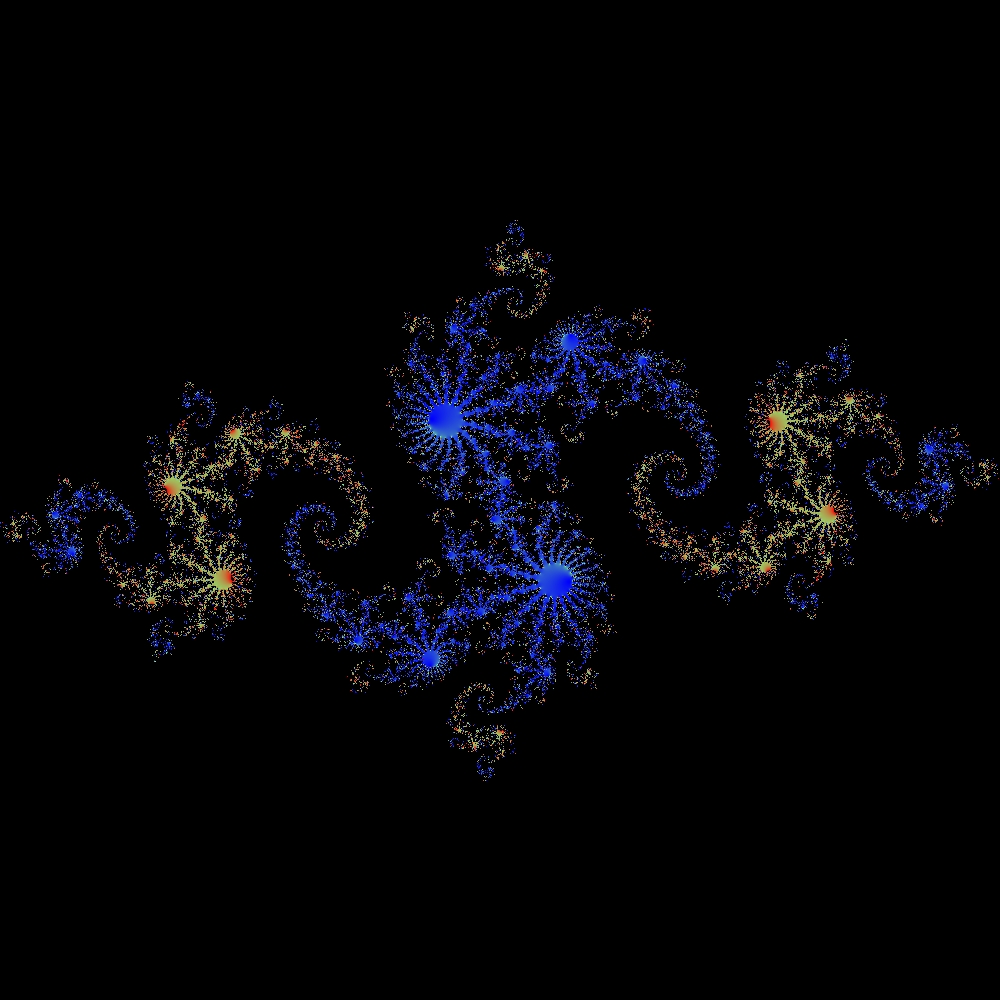
Fractals
This software uses Newton’s method (the one from any first year calculus course) in the complex plane to generate fractals. This code makes use of many of the new C++11 language features, so a newer compiler will be required (I used GCC 4.8.1 running on Opensuse). This code is documented …