A Statistical Model for Designers of Rate Monotonic Systems
Paul S.
Heidmann
Computing
Devices International
8800
Queen Av. S.
Bloomington,
Mn 55431-1996
(612)
921-7377
paul.s.heidmann@cdev.com
Introduction
In designing Rate Monotonic
systems, developers have had difficulty predicting the schedulability of a
given system during the design phase.
Typically, upper bounds (usually pessimistic) for the parameters of the
Rate Monotonic equations are estimated based upon expected behavior. If calculations then show that the
(estimated) system will not be schedulable, designers modify the estimates in
an attempt to ascertain what will be required to achieve schedulability. This ad hoc approach has the disadvantages of
assuming that the parameters are fixed and of providing the designer with
little quantitative information.
The model presented in this
paper provides a partial solution to these problems. The model replaces the fixed parameter of
task execution time with a statistical distribution in the Rate Monotonic
equations. Used in tandem with
traditional Rate Monotonic calculations during the design phase provides
quantitative information about the impact of varying execution times. This information in turn may be used to
perform risk analysis and schedulability impact studies.
Also presented in this paper is
an application of this model to an example task set. The effects of the perturbation of parameters
are demonstrated. Varying the means in
the defining distributions is shown to have the greatest impact on
schedulability.
The Model
in Detail
This section presents the model
used in detail. Motivation will be given
for the modeling choices made. The model
will then be derived, with proofs given for the significant statements.
Motivation for the Modeling Choices Made
In modeling the execution times
of computer processes, care must be taken to allow for diverse behavior. The variance of the execution time of each
job with its inputs must be taken into account.
Furthermore, the characteristics of that variance will vary from process
to process (e.g. the execution times of different processes may need to be
modeled with different distributions).
It is also desirable to maintain some commonalty between the different
distributions used to model the different processes as this simplifies
computations and analysis.
To these ends, pieces of normal
distributions have been chosen to model the execution times of tasks. For each process, upper and lower bounds on
the possible execution times are first chosen.
Next, a normal distribution (with distinct 
[1] and 
) is chosen for the process.
The process's distribution is then defined to be that part of the normal
distribution that lies between the upper and lower bounds (multiplied by a
constant).
Derivation of the Model
A task set is schedulable, by
the Rate Monotonic Scheduling Theory, if the following condition is met:
where the 
's are the task execution times, the 
's are the task periods, and the 
's are the task blocking times.
Initially, the PDF (probability
density function) for a piece of a normal distribution must be determined. This amounts to deriving the appropriate
constant, 
, such that:
.
Where 
is the desired piece
of the normal distribution 
with mean and variance 
. is then readily found:
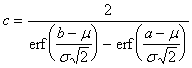
At this point, we have derived
the PDF for this distribution:
The expected value of the
random variable 
described by this
distribution can then be shown to be:
.
Now, let 
be 
stochastically
independent[2] random variables each described by the above
distributions (e.g. each random variable is described by the above distribution
with distinct 
, 
, 
's, and 
's). To determine the
probability of schedulability, the PDF of the sum of these random variables is
required. Define the random variable 
as follows:
,
where the 
's are positive. It is
now necessary to find the PDF for the random variable . To this end, define 
. These functions
define a one to one transformation from the space
to the space
Now define the following the
following set of functions:
These functions define a one to
one transformation from the space 
to the space 
. Because of the
assumption that task execution times are stochastically independent, the joint
PDF of all task execution times will simply be:
,
where 
is the PDF of the
random variable 
. Using a theorem from
analysis (see [1, p. 288-289] for the two and three dimensional cases), we have
the following:
,
where 
is the Jacobian of the
transformation defined by the functions 
. In this case,
.
This, however, gives the joint
PDF of the random variables 
:
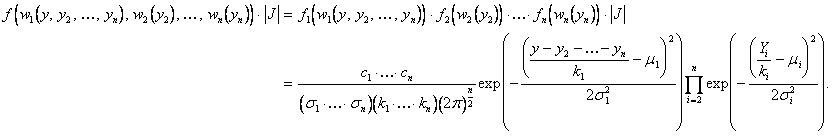
The extraneous variables 
can now be integrated
out of the above joint PDF, giving the desired PDF of the variable 
. To accomplish this,
the limits of integration must first be determined. To this end, define the following:
Finally, the PDF of the desired
variable, , can be stated:
Using this PDF, the
characteristics of a sum of random variables described by pieces of normal
distributions is known. It now remains
to characterize the minimum of a collection of these sums. Let 
be a collection of
sums of random variables described by pieces of normal distributions. Let 
be the event 
, then
.
The following lemma can now be
used to find 
:
Lemma: Let 
be events. Then,
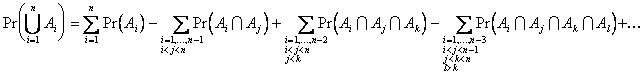
Proof: By induction.
Consider first the 
case:
.
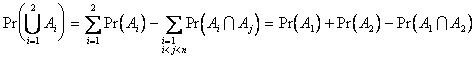Now, assume the above holds for ; show the expression then holds for 
:
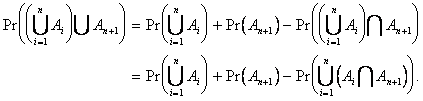
Apply the inductive hypothesis
to 
:
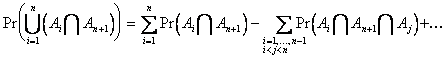
Also apply the inductive
hypothesis to 
. Combining then gives
the desired result.
By setting the s to the appropriate values, and computing the integrals
numerically, the results presented here are used to predict schedulability and
study the effects of parameter perturbations in a Rate Monotonic system.
Parameter Perturbations
This section demonstrates the
impact of the perturbation of the parameters that characterize task execution
times on schedulability. Specifically, a
task set is defined with fixed bounds on the minimum and maximum execution time
for each task. The parameters defining
how the task execution times are distributed between the respective minimum and
maximum are then varied, and the effects shown.
The following task set is used
in the example presented here:
|
Task |
Min
Exec Time |
Max
Exec Time |
Period |
|
1 |
38 |
42 |
100 |
|
2 |
38 |
42 |
150 |
|
3 |
98 |
102 |
350 |
|
|
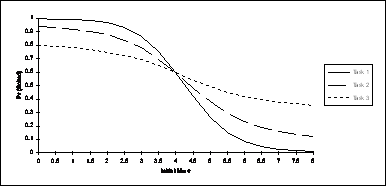
First, the effect of varying
the means of the normal distributions, pieces of which describe the execution
times, is shown. The graph should be
interpreted as follows: The line labeled
Task 1 shows the probability of
schedulability[3] as the mean of the distribution describing
task 1 is increased (along the x-axis) from an initial value of 
[4] to 
.[5] While the mean of the distribution of task 1
is varied, the means of tasks 2 and 3 are held constant 
. The line labeled Task 2 shows the probability of
schedulability as the mean of the distribution describing task 2 is varied from
to (while 
and 
). Similarly, the line
labeled Task 3 shows the probability
of schedulability as the mean of the distribution describing task 3 varies from
to 
(as 
are held
constant). The standard deviations of
the distributions were held constant at 
.
|
|
Second, the effect of varying
the standard deviations of the normal distributions, pieces of which describe
the execution times, is shown. This graph
should be interpreted as follows: The
line labeled Task 1 is the
probability of schedulability as the standard deviation of the distribution
describing task 1 is varied (along the x-axis) from 
to 
. While 
is varied, 
and 
are held constant at a
value of 1.0. Similarly, the lines
labeled Task 2 and Task 3 show the effects of varying and , both from 0.5 to 3.0, respectively (with 
and 
held constant at 1.0,
respectively). The means of the
distributions are held constant at and .
Using the techniques presented
in this section, the developer is able to perform sensitivity analysis on a
given task set. This information may be
used to provide risk analysis during the design phase, before the exact
execution times are known.
Future Research
This section discusses possible
areas for future research.
Further development of the
model is certainly required if it is to be as realistic as possible. Blocking time could be modeled with the same
types of distributions as execution times.[6] Interrupt arrivals could be modeled using a
discrete distribution. Sporadic server
depletion could then be characterized.
Tasks with soft deadlines may
be modeled as well. Using the paradigm
presented, the probability of a deadline being met for a task with a soft
deadline may be characterized.
Tasks with the capability of
performing imprecise calculations (see [2]) may also be modeled. Here, the model may be used to characterize
average accuracy of the results of any given task.
Conclusion
In this paper a paradigm for
modeling Rate Monotonic systems is derived.
This paradigm is then used to demonstrate the effects of varying task
execution time characteristics. The
means of the distributions are seen to have the greatest impact. Standard deviations demonstrate some impact
on schedulability, but it is seen to be rather minor in most cases.
Future development of the model
will be required for complete characterization of most real-time systems. The inclusion of blocking time will be
required, as well as a method for modeling the arrival of interrupts.
Bibliography
[1] Kaplan, Wilfred
Advanced Calculus
Addison-Wesley Publishing Company, 1952
[2] Liu, Jane W. S., Lin, Kwei-Jay, Natarajan, Swaminathan
Scheduling
Real-Time, Periodic Jobs Using Imprecise Results
Proceedings of the Real-Time Systems Symposium, 1987
Acknowledgment
The author wishes to thank
Dwight Galster for his many helpful comments and suggestions.