THE
PERFORMANCE OF THE EPSILON AND THETA CONVERGENCE ACCELERATION ALGORITHMS
A Paper
Submitted to the Graduate Faculty
of the
North Dakota State University
of Agriculture and Applied Science
By
Paul Scott Heidmann
In Partial Fulfillment of the Requirements
for the Degree of
MASTER OF SCIENCE
Major Department:
Mathematics
August 1992
Fargo, North Dakota
THE PERFORMANCE OF THE EPSILON AND THETA CONVERGENCE ACCELERATION ALGORITHMS
By
Paul Scott Heidmann
The Supervisory Committee certifies that this paper complies with North Dakota State University's regulations and meets the accepted standards for the degree of
MASTER OF SCIENCE
SUPERVISORY COMMITTEE:
___________________________________________________________________
Chair
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
Approved by Department Chair:
___________________ __________________________________
Date Signiture
Abstract
Heidmann, Paul Scott, M.S., Department of Mathematics, College of Science and Mathematics, North Dakota State University, August 1992. The Performance of the Epsilon and Theta Convergence Acceleration Algorithms. Major Advisor: Associate Professor Davis Cope.
Motivations
for transforms are first presented, along with the derivation of both the ![]() -algorithm and the
-algorithm and the ![]() -algorithm. Known
properties are then presented, with a partial classification of the sets for
which the transforms are known to have accelerative properties.
-algorithm. Known
properties are then presented, with a partial classification of the sets for
which the transforms are known to have accelerative properties.
Empirical
evidence is given illustrating the performance of the algorithms over a broad
set of test series. The ![]() -algorithm was found to perform better than the
-algorithm was found to perform better than the ![]() -algorithm on all but a few of the test cases
considered. No algorithm considered
demonstrated any evidence of producing an increase in the exponential rate of
convergence. No evidence of instability
was seen among the algorithms considered.
-algorithm on all but a few of the test cases
considered. No algorithm considered
demonstrated any evidence of producing an increase in the exponential rate of
convergence. No evidence of instability
was seen among the algorithms considered.
Table Of Contents
Abstract................................................................................................................................ iii
Section 1: Introduction........................................................................................................... 1
Section 2: Transform Motivations and Properties.................................................................... 4
The Motivation of the e Transform................................................................. 4
Properties of the e Transform......................................................................... 7
The e Transform and the -Algorithm........................................................... 10
The Motivation of the q Transform............................................................... 13
Properties of the q Transform....................................................................... 14
Section 3: Empirical and Related Results.............................................................................. 16
Details of the Test Program.......................................................................... 17
Details of Test Procedures........................................................................... 17
Transform Singularities................................................................................. 18
Empirical Results......................................................................................... 23
Group 1.......................................................................................... 23
Group 2.......................................................................................... 77
Group 3.......................................................................................... 80
Group 4.......................................................................................... 95
Group 5........................................................................................ 101
Group 6........................................................................................ 115
Group 7.....................................................................................117
Section 4: Summary........................................................................................................... 126
Bibliography...................................................................................................................... 127
Section 1
Introduction
This paper is concerned with the evaluation of the performance of the -algorithm and the -algorithm when applied to sequences of partial sums. Transform definitions and properties are first stated, followed by empirical examples illustrating the comparative performance of the algorithms on a wide variety of test problems.
The two transforms covered in this paper are recursive and operate on the set of complex valued nonconstant sequences. For broad classes of sequences, these algorithms are known to have accelerative properties.
Both algorithms are actually more accurately described as a hierarchy of transforms. That is, the algorithms provide a succession of transforms, with the higher order transforms typically providing greater rates of acceleration.
The
first of these algorithms, the -algorithm, is defined as
follows for any nonconstant sequence ![]() [6, p. 225]:
[6, p. 225]:
![]()
![]() .
.
The
second algorithm considered in this paper is the -algorithm, defined as follows
for any nonconstant sequence ![]() [6, p. 225]:
[6, p. 225]:
![]()
![]()
![]()
In most practical applications, a transform must have the properties of regularity and of convergence acceleration. This paper was concerned more with the latter than the former; however, both definitions will be required.
Definition: A transform T is said to be regular for a convergent sequence sn if
![]()
Definition: A transform T is said to accelerate the convergence of a sequence sn if
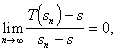
where s is the limit of the sequence sn.
Intuitively, a transform accelerates the convergence of a sequence if the convergence of the transformed sequence is of higher order than that of the original sequence. Equivalently, a transform accelerates the convergence of a sequence if the error term of the transformed sequence asymptotically goes to zero with a higher order than the error term of the original sequence.
Section 2 of this paper summarizes the known properties of the transforms. The transforms are first motivated, and then theorems concerning each are presented.
Section 3 presents two new lemmas and presents the empirical research done in connection with this paper.
Section 4 summarizes the results reached in Section 3.
Section 2
Transform Motivations and Properties
The Motivation of the e Transform
The history
of the e transform is not altogether clear.
The general ideas which underlie this transform go at least as far back
as Jacobi. A special case of the e transform known as the ![]() -process is usually attributed to Aitkin; however, this
technique can be traced back to Kummer (1837) [8, p. 120]. Apparently, it was developed independently by
several authors (although not always in its most general form): Delaunay, Samuelson, Shanks and Walton,
Hartee, and Isakson [5, p. 5].
-process is usually attributed to Aitkin; however, this
technique can be traced back to Kummer (1837) [8, p. 120]. Apparently, it was developed independently by
several authors (although not always in its most general form): Delaunay, Samuelson, Shanks and Walton,
Hartee, and Isakson [5, p. 5].
The e transform has been motivated by two distinct but similar sets of ideas. Both begin with the recognition that many sequences in applied mathematics and physics can be approximated by a limit together with exponential transients:
![]() .
.
Here, it is assumed that none of the ![]() 's are zero or one (if a transient were one, it would become
part of the limit s) and that the
's are zero or one (if a transient were one, it would become
part of the limit s) and that the ![]() 's are distinct. The
elemental idea is to develop a transform which will eliminate these exponential
transients.
's are distinct. The
elemental idea is to develop a transform which will eliminate these exponential
transients.
The first
method of accomplishing this task was given by Shanks [5, p. 7-8] and is
summarized below. Observe that any
nonsingular sequence (definition follows) can be expressed as a kth order transient locally. Fix any n
larger than k and represent ![]() as follows:
as follows:
![]() ,
,
where the ![]() 's are the respective limits, called the "kth order local bases." Should one of the
's are the respective limits, called the "kth order local bases." Should one of the ![]() , then the sequence will be singular.[1] These bases will vary relatively little as
long as
, then the sequence will be singular.[1] These bases will vary relatively little as
long as ![]() is nearly kth order [5, p. 7]. This fact suggests that the sequence of
is nearly kth order [5, p. 7]. This fact suggests that the sequence of ![]() 's (for some fixed k)
might converge faster than the sequence itself. This sequence of kth
order local bases is then defined as the
's (for some fixed k)
might converge faster than the sequence itself. This sequence of kth
order local bases is then defined as the ![]() -transform of the sequence
-transform of the sequence ![]() [5, p. 8], [in fact,
it is identical with
[5, p. 8], [in fact,
it is identical with ![]() as defined in the
following discussion.]
as defined in the
following discussion.]
The motivation for the e transform given by Wimp [8, p. 121-123] also begins with the recognition that many sequences from applied mathematics and physics behave as if they were a limit combined with exponential transients. As above, the e transform is then developed to eliminate these transients; the technique by which the transform is developed, however, differs significantly.
To begin
(as above), assume the sequence ![]() has the form:
has the form:
![]() .
.
To simplify notation, let:
![]() .
.
Since ![]() is a linear
combination of k exponentials, there
is a linear difference operator of order k
that annihilates
is a linear
combination of k exponentials, there
is a linear difference operator of order k
that annihilates ![]() :
:
![]() (
(![]() not zero).
not zero).
Now, rewrite ![]() as follows:
as follows:
![]() .
.
Next, substitute into the difference equation, and solve for
![]() .[2] Redefining constants gives:
.[2] Redefining constants gives:
![]() .
.
This is a homogeneous system of equations with a nonzero
solution ![]() . Such a solution
will exist if and only if the following determinental equation is satisfied:
. Such a solution
will exist if and only if the following determinental equation is satisfied:
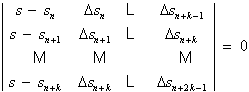 .
.
For simplicity, define:
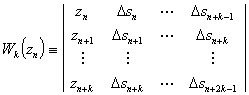 .
.
Then, solving for s gives [8, p. 122]:
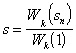 .
.
While the above equation will only be valid for sequences
that can be represented as a combination of a limit and exponential transients,
it can nevertheless be used to define a transform useful for a much larger
class of sequences, which is written ![]() .
.
While these two derivations are quite different, they are indeed equivalent [5, p. 2-3,7-8].
Properties of the e Transform
At this point, several questions naturally arise. Questions concerning the regularity of the transform, the accelerative properties, and optimality are especially significant. This section presents known results that address these questions.
The first question that must be answered before the e transform can be used in any application is whether or not the transform will be regular for the sequences involved. For many applications, this question will not be difficult to answer, as the e transform can be shown to be regular on broad classes of sequences.
The following theorem (accredited originally to Lubkin) is stated by Shanks [5, p. 13]:
Theorem: If ![]() and
and ![]() both converge, then
both converge, then
![]() .
.
Further regularity results are available for this transform
and are discussed in the ![]() -algorithm section.
-algorithm section.
Closely related to the question of regularity is the question of exactness. That is, for what class of sequences will the e transform be exact (produce the limit of the sequence in a finite number of steps)? This question is answered in part by the following theorem, given by Shanks [5, p. 22]:
Theorem: Let f(z)
be a rational function, which when reduced to its lowest terms has a q'th degree numerator and a p'th degree denominator; then, if ![]()
![]() ,
,
where ![]() is the first n terms of the Taylor expansion for f.
is the first n terms of the Taylor expansion for f.
In fact, a closely related but stronger theorem has been given by Wimp [8, p. 125]:
Theorem: ![]() is defined for
all
is defined for
all ![]() and
and ![]() if and only if
if and only if ![]() satisfies a
homogeneous linear difference equation of order k with constant coefficients (and no equation of lower order) and
satisfies a
homogeneous linear difference equation of order k with constant coefficients (and no equation of lower order) and ![]() contains no terms
that are purely algebraic..
contains no terms
that are purely algebraic..
Finally, questions of optimality and accelerative properties must be addressed. Here, while fewer results are known, it is still possible to partially characterize sequences for which e is accelerative. A definition along with two helpful theorems are stated:
Definition: Let ![]() be the terms of a
convergent series with partial sums
be the terms of a
convergent series with partial sums ![]() and sum S.
Let
and sum S.
Let ![]() , and suppose that the sequences
, and suppose that the sequences ![]() converge to
converge to ![]() , respectively. The
convergence of the series is said to be logarithmic
if
, respectively. The
convergence of the series is said to be logarithmic
if ![]() , linear if
, linear if ![]() , and of higher order
if
, and of higher order
if ![]() [6, p. 224].
[6, p. 224].
The following two theorems are very useful for determining
whether or not the condition ![]() is satisfied:
is satisfied:
Theorem: If ![]() is of constant sign,
then
is of constant sign,
then ![]() [3, p. 26].
[3, p. 26].
Theorem: If ![]() with
with ![]() and if r is not -1, then
and if r is not -1, then ![]() [3, p. 26].
[3, p. 26].
Wimp has
shown [8, p. 104] that ![]() will accelerate all
linearly convergent series. More
interesting, however, are the results produced by Delahaye. Three basic results concerning the
optimality of the
will accelerate all
linearly convergent series. More
interesting, however, are the results produced by Delahaye. Three basic results concerning the
optimality of the ![]() transform (Aitkin's
transform (Aitkin's ![]() process) on the
family of linearly convergent series are presented [4, p. 213]:
process) on the
family of linearly convergent series are presented [4, p. 213]:
1. The ![]() transform is
algebraically optimal; that is, it is not possible to find an algebraically
simpler transform to accelerate the family of linearly convergent series.
transform is
algebraically optimal; that is, it is not possible to find an algebraically
simpler transform to accelerate the family of linearly convergent series.
2. It is impossible to accelerate the linear
family with degree[3]
greater than 1, the degree of acceleration achieved with the ![]() transform.
transform.
3. The linear family cannot be enlarged into
another accelerable family. That is,
there does not exist a family of sequences containing the linear family for
which ![]() can be shown to have
the above properties.
can be shown to have
the above properties.
Delahaye then interprets these facts [4, p. 213]:
These results do not mean that the ![]() is the best algorithm
of acceleration. They only mean that
concerning the family Lin, it is impossible to find a simpler or a more
efficient algorithm of acceleration.
This does not contradict the existence of subfamilies of Lin accelerable
with degree 2, nor does it contradict the existence of algorithms less simple
but equally efficient on Lin.
is the best algorithm
of acceleration. They only mean that
concerning the family Lin, it is impossible to find a simpler or a more
efficient algorithm of acceleration.
This does not contradict the existence of subfamilies of Lin accelerable
with degree 2, nor does it contradict the existence of algorithms less simple
but equally efficient on Lin.
The e Transform and the 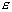 -Algorithm
-Algorithm
When first developed, the e transform was merely a curiosity. It had little practical value, as calculating the large order determinants inherent to the transform was computationally prohibitive. This changed in 1956 when Wynn produced the following theorem [9, p. 91]:
Theorem: If
![]()
and
![]() ,
,
then
![]()
provided that none of the quantities ![]() becomes infinite.
becomes infinite.
With this algorithm, it is now possible to compute the e transform easily and efficiently. Study of the -algorithm has also facilitated much knowledge of the e transform.
One such result is due to Wimp. However, before stating this result, two definitions are required :
Definition: A sequence s is totally monotone (written ![]() ) if
) if
![]() .
.
Definition: A sequence s is totally oscillatory (written ![]() ) if
) if
![]() [8, p. 12].
[8, p. 12].
Theorem: Let the sequence s have remainder terms r;
then, if r is either totally monotone or totally oscillatory, then ![]() is regular for all
even m [8, p. 139 and 141].
is regular for all
even m [8, p. 139 and 141].
While the
algorithm is regular for large classes of sequences, this is not the only
concern. Computing the transform involves
repeated divisions by what can be very small quantities. This seems to suggest that the transforms
will be prone to numerical instability.
However, the empirical results presented in this paper suggest that the ![]() -algorithm is far more stable than appears at first.
-algorithm is far more stable than appears at first.
Theoretical
analysis of the stability of the ![]() -algorithm has not yet been fully developed. However, Wynn has presented a paper that
begins to deal with this issue [10].
The results presented suggest that the
-algorithm has not yet been fully developed. However, Wynn has presented a paper that
begins to deal with this issue [10].
The results presented suggest that the ![]() -algorithm can be unstable for certain monotonic sequences
[10, p. 110-112] and unconditionally stable for certain oscillating sequences
[10, p. 112-115]. These theoretical
results can be seen intuitively, simply by examining the transform. Oscillating sequences have adjacent terms
opposite in sign. This tends to make
the denominator in the defining recurrence relation larger. Monotonic sequences have terms of like sign,
which in turn tends to make the denominator smaller.
-algorithm can be unstable for certain monotonic sequences
[10, p. 110-112] and unconditionally stable for certain oscillating sequences
[10, p. 112-115]. These theoretical
results can be seen intuitively, simply by examining the transform. Oscillating sequences have adjacent terms
opposite in sign. This tends to make
the denominator in the defining recurrence relation larger. Monotonic sequences have terms of like sign,
which in turn tends to make the denominator smaller.
Finally,
the ![]() -algorithm can be shown to be closely related to the Padé
table. The Padé table for an analytic
function f is a two dimensional table
of rational approximations of f. The [L,M] entry of the Padé table is
typically denoted [L/M] and is defined as follows [1, p. 5]:
-algorithm can be shown to be closely related to the Padé
table. The Padé table for an analytic
function f is a two dimensional table
of rational approximations of f. The [L,M] entry of the Padé table is
typically denoted [L/M] and is defined as follows [1, p. 5]:
![]() ,
,
where ![]() is a polynomial of
degree at most L and
is a polynomial of
degree at most L and ![]() is a polymonial of
degree at most M. The coeficients of the polynomials are
chosen so that
is a polymonial of
degree at most M. The coeficients of the polynomials are
chosen so that ![]() , where A(z) is the
Taylor expansion of f(z) [6, p.
5]. If we require that Q and P have no common factors and that Q(0) = 1, then [L/M] is unique [1, p. 8].
, where A(z) is the
Taylor expansion of f(z) [6, p.
5]. If we require that Q and P have no common factors and that Q(0) = 1, then [L/M] is unique [1, p. 8].
The ![]() -algorithm produces certain entries in the Padé table. The following theorem then is due to Wynn
[10, p. 93]:
-algorithm produces certain entries in the Padé table. The following theorem then is due to Wynn
[10, p. 93]:
Theorem: If the ![]() -algorithm is applied to the initial values
-algorithm is applied to the initial values
![]() ,
,
then
![]() .
.
The Motivation of the Transform
The transform was developed by Brezinski as a means of accelerating the convergence of logarithmically converging sequences. Its motivation began with the observation that the algorithm fails to accelerate convergence on large classes of logarithmically converging sequences. However, rather than developing a completely new transform, Brezinski opted to modify the algorithm, adding an optimizing parameter.
Define ![]() . Then it is known
that a set of sequences with logarithmic convergence having the property
. Then it is known
that a set of sequences with logarithmic convergence having the property
![]()
may be accelerated by the algorithm modified with a "parameter of acceleration" [2, p. 727], specifically, with the following transform:
![]()
![]()
A necessary and sufficient condition for ![]() to converge faster
than
to converge faster
than ![]() is to take
is to take
![]()
However, calculating all of the ![]() parameters can be
prohibitive. It was at this point that
Brezinski took his departure from what was then known. His idea was to replace
parameters can be
prohibitive. It was at this point that
Brezinski took his departure from what was then known. His idea was to replace ![]() with the following
approximation [2, p. 729]:
with the following
approximation [2, p. 729]:
![]()
The transform then results.
Properties of the Transform
A property important in the application of any transform is regularity. Brezinski has characterized this property with the following theorem [2, p. 730]:
Theorem: For real valued sequences, a necessary and sufficient condition for
![]()
is that
![]()
As to the transform's accelerative properties, two theorems are given here. The first, and less general theorem, results from Germain-Bonne's theorem and is given by Smith and Ford [6, p. 225]:
Theorem: ![]() accelerates linear
convergence.
accelerates linear
convergence.
The second theorem, due to Brezinski [2, p. 730], is much farther reaching:
Theorem: If is regular and if ![]() exists and is finite,
then
exists and is finite,
then ![]() converges faster than
converges faster than
![]() .
.
Finally,
the question of exactness is addressed by a theorem due to Cordellier and
stated by Smith and Ford [6, p. 229].
It should be noted that this theorem characterizes only those sequences
for which ![]() is exact in one term.
is exact in one term.
Theorem: ![]() for
for ![]() if and only if the
sequence
if and only if the
sequence ![]() is one of the
following three types:
is one of the
following three types:
1. ![]() where
where ![]()
2. 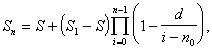 where
where ![]() and neither
and neither ![]() is a positive
integer.
is a positive
integer.
3. ![]() and d is not a positive integer.
and d is not a positive integer.
Section 3
Empirical and Related Results
This section describes the empirical research done in connection with this paper. Many series[5] were computed, and the transforms were applied to the sequences of their partial sums. The error terms for the sequences of partial sums, as well as the transformed sequences, were plotted. This allowed observations to be made concerning acceleration rates, stability, and unusual behavior (where it occurred).
Special software was constructed as arbitrary precision proved to be necessary. The high amount of precision was required for different reasons. Many of the transforms achieved upwards of 35 places of precision in only 30 terms. Other series were chosen to be very close to singular values for the transforms. Also, the high precision allowed elimination of numerical problems, so the properties of the transforms could be easily studied.
Details of the Test Program
This section describes the program used to perform the calculations involved in constructing the many examples presented in this paper.
As many precision problems can arise during the calculation of these transforms, arbitrary precision was necessary for the observation of the behavior of the transforms considered in this paper.
The storage of arbitrary length numbers was accomplished using linked lists. Specifically, the numbers were stored as linked lists of bytes, each byte containing two digits. Also, since the transforms operate on sequences, it was necessary to store sequences of these arbitrarily long numbers. This was accomplished in a similar manner, using linked lists. Finally, subroutines were added to perform arithmetic functions and transforms on these arbitrarily long sequences of arbitrarily long numbers.
Details of Test Procedures
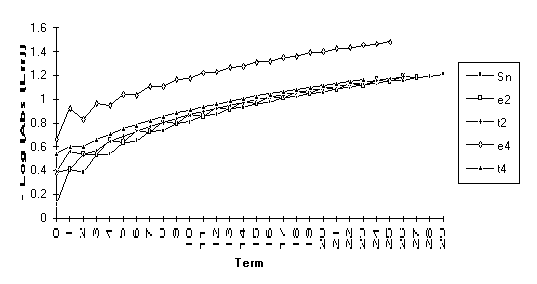
Following are several graphs illustrating the results of the empirical research done. All graphs are plots of the log (base 10) of the absolute value of the error. This configuration allows the approximate number of digits accurately calculated to be viewed at a glance.
The graphs contain two types of information. First, there is the size of the error term for each of the series and their transforms. Secondly, the rate of exponential acceleration can be seen in the slope of the corresponding line.
The actual value that any series under consideration converges to must be known. For those series which proved to have a reasonable rate of convergence, this limit was computed simply by summing the series out to several hundred terms before the transforms were computed. For those series with slower rates of convergence, Kummer acceleration was used to arrive at the limit. Several series had to be eliminated from the test set because their limit could not be computed.
Many
of the series contained a term ![]() . Where it was found,
this modifier was defined as follows:
. Where it was found,
this modifier was defined as follows:
![]() .
.
The ![]() 's provided a nonrational factor that did not change the
value of
's provided a nonrational factor that did not change the
value of 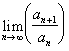 .[6]
.[6]
Transform Singularities
In this section, two lemmas are given that demonstrate that it is possible for the transforms to have singularities. Two illustrations are also be given to demonstrate the behavior of the transforms near a singularity.
Lemma:
Apply the ![]() -algorithm to the sequence
-algorithm to the sequence ![]() . Then,
. Then, ![]() is undefined if
is undefined if ![]() .
.
Proof: From the defining equations,
![]() .
.
However, since ![]() is a sequence of
partial sums,
is a sequence of
partial sums,
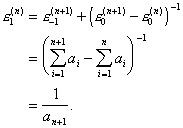
Combining the above,
![]() .
.
This will be
undefined whenever ![]() .
.
Remarks:
1. If the
sequence in question is a power series of the form ![]() , then
, then ![]() will be undefined at
will be undefined at ![]() .
.
2. This result
may be generalized to an arbitrary sequence ![]() . The nth term of
. The nth term of ![]() will be undefined
when
will be undefined
when ![]() .
.
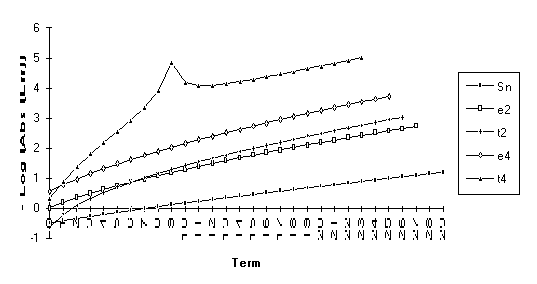
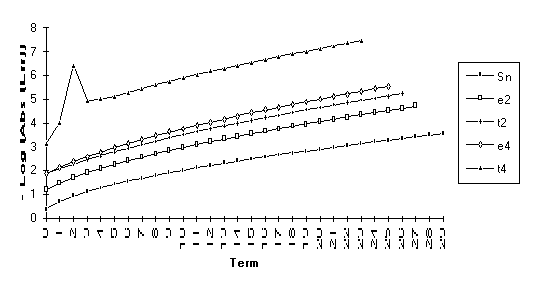
The
following graph illustrates the above lemma.
The numeric value used here was chosen to be very near to the value that
would cause ![]() to be undefined. As can easily be seen, this sort of behavior
cannot be ignored in practical applications of this algorithm.
to be undefined. As can easily be seen, this sort of behavior
cannot be ignored in practical applications of this algorithm.
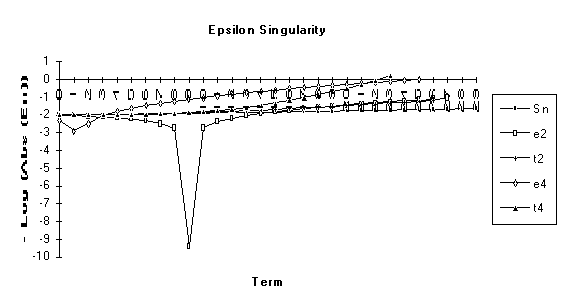
![]()
Analogously, a similiar lemma can be proven for the algorithm:
Lemma:
Apply the ![]() -algorithm to the sequence
-algorithm to the sequence ![]() . Then,
. Then, ![]() is undefined if
is undefined if ![]() .
.
Proof: From the defining equations,
![]() .
.
This will be
undefined when ![]() .
.
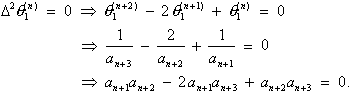
Remarks:
1. If the
sequence of partial sums is a power series of the form ![]() , then
, then ![]() is undefined at
is undefined at ![]() .
.
2. This result
may be generalized to an arbitrary sequence ![]() . In this case,
. In this case, ![]() is undefined if
is undefined if ![]() where
where ![]() .
.
The following chart illustrates the
above lemma. The numeric value used
here was chosen to be very close to the value that would make ![]() undefined. As before, this behavior cannot be ignored
if the algorithm is to be used in practice.
undefined. As before, this behavior cannot be ignored
if the algorithm is to be used in practice.
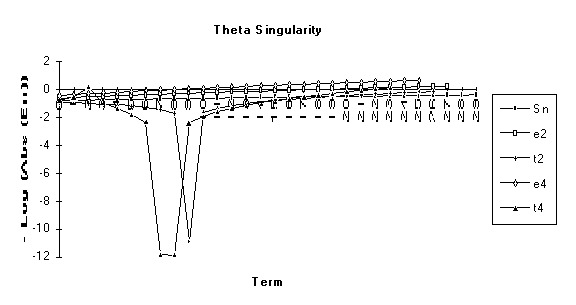
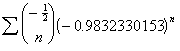
Other examples of how these singularities affect the behavior of the transforms have been computed, but they are not included here as the behavior is the same in all examples considered.
Empirical Results
Group 1
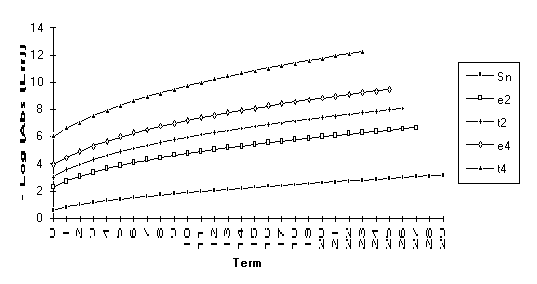
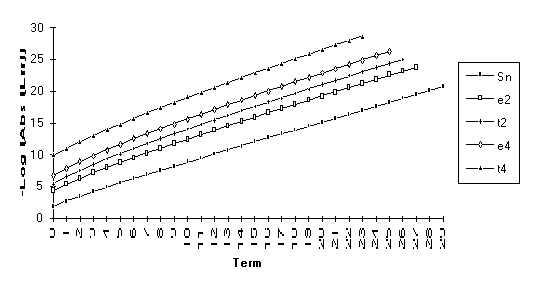
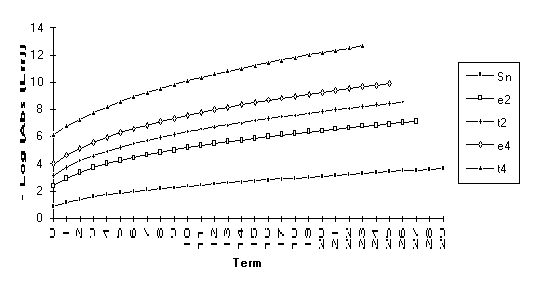
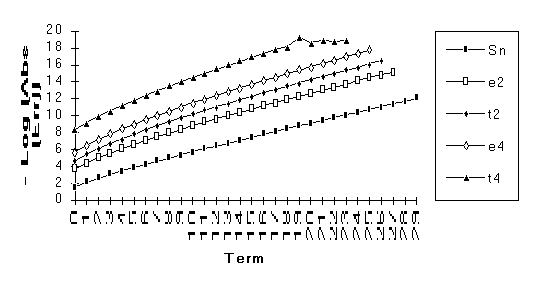
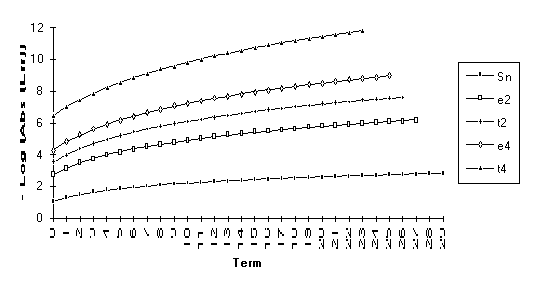
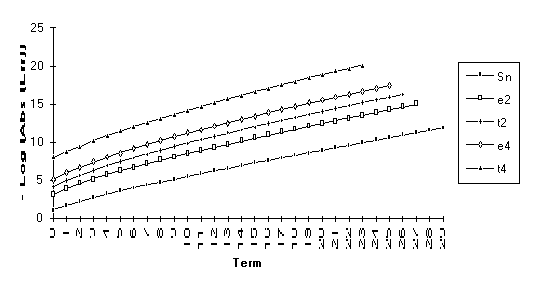
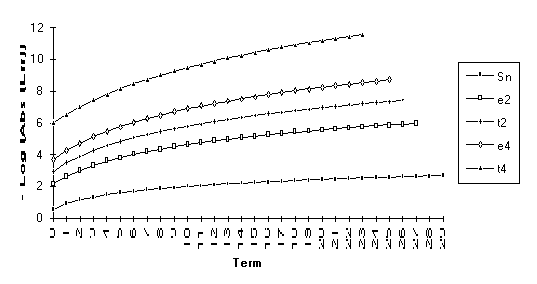
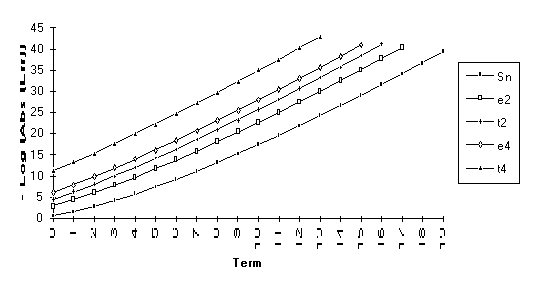
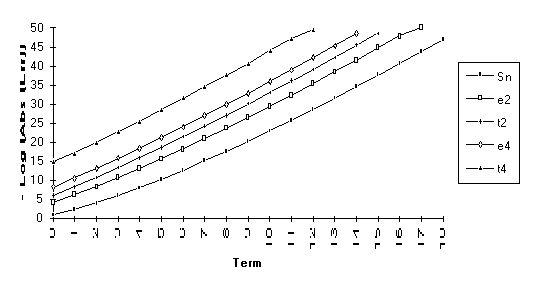
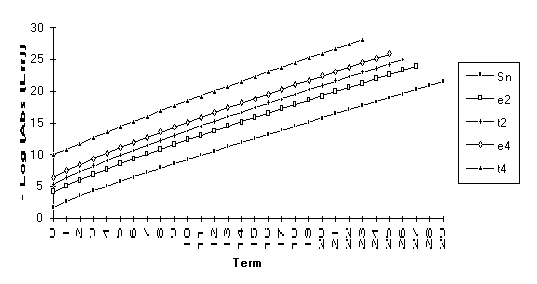
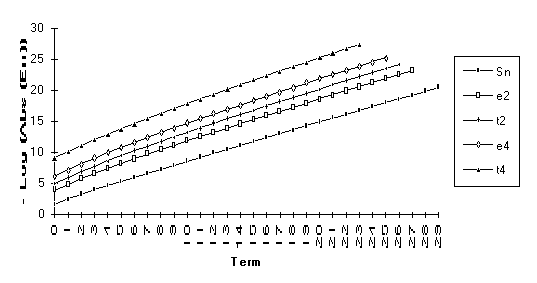
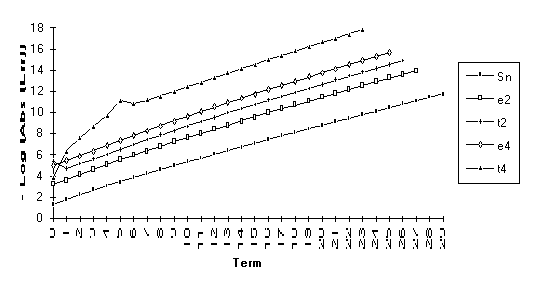
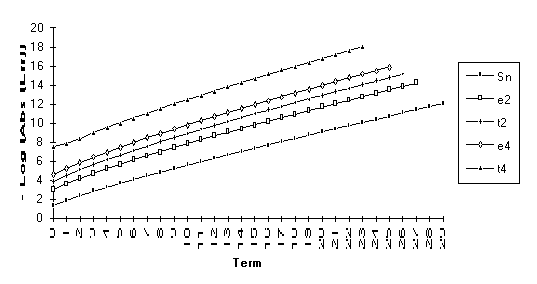
This
set consists of those series for which the following order of performance can
be clearly seen (from best to worst): ![]() . This is by far the
largest group, suggesting that the
. This is by far the
largest group, suggesting that the ![]() -algorithm generally outperforms the
-algorithm generally outperforms the ![]() -algorithm.
-algorithm.
![]()

![]()
![]()
![]()
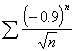
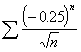

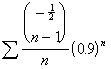
![]()
![]()

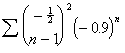
![]()
![]()
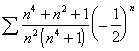
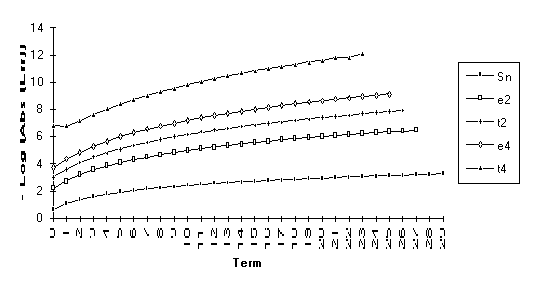
![]()
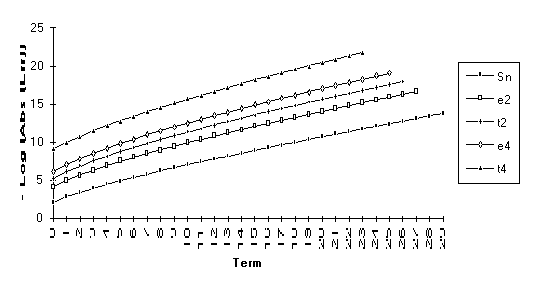
![]()

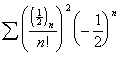
![]()
![]()
![]()
![]()
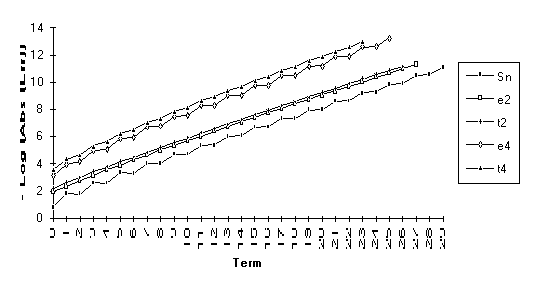
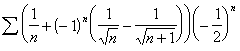
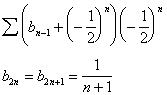

![]()
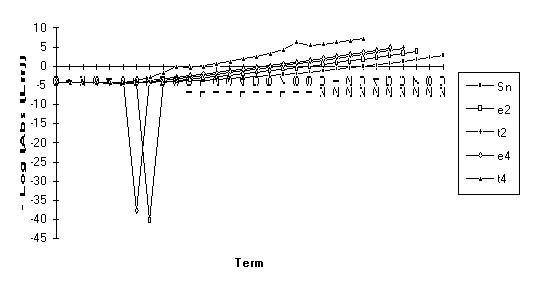
![]()
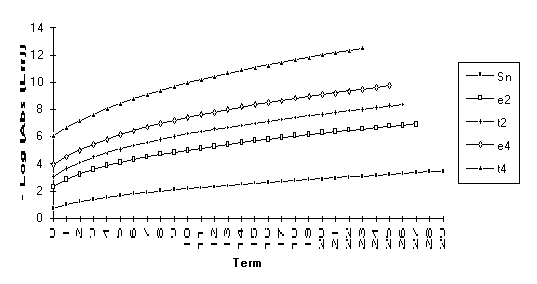
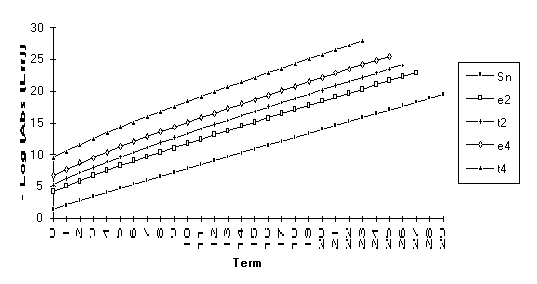
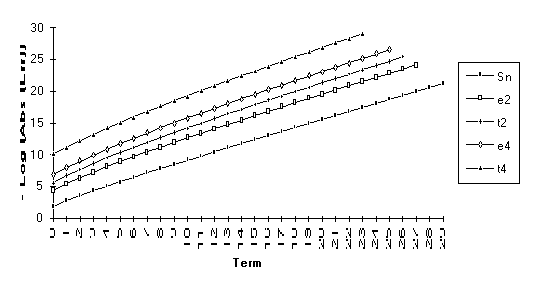
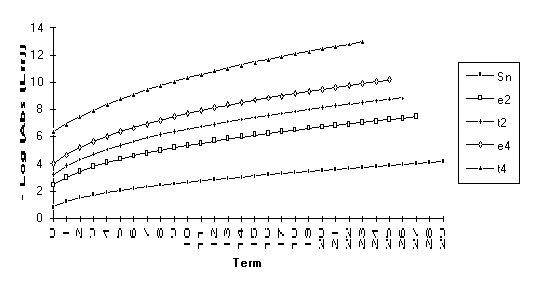
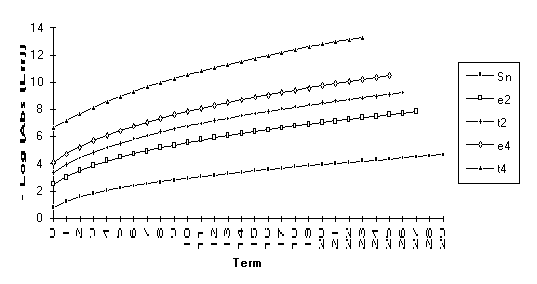
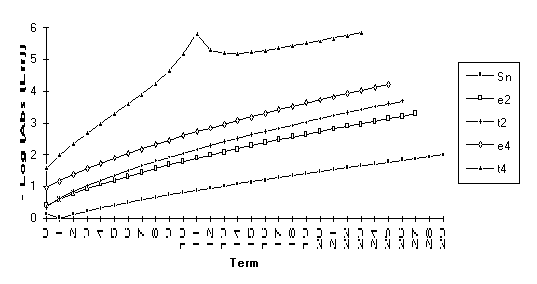
The anomoly in this graph is due to
the fact that ![]() is nearly undefined
(as discussed at the end of Section 3).
is nearly undefined
(as discussed at the end of Section 3).

Note: Calculations made with 50 places of precision.
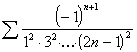
Note: Calculations made with 50 places of precision.
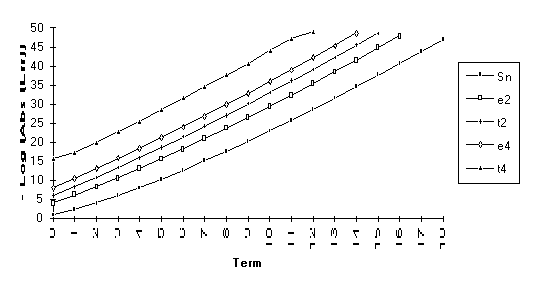
![]()
Note: Calculations made with 50 places of precision.
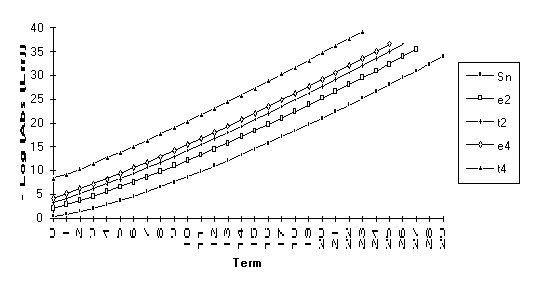
![]()

![]()
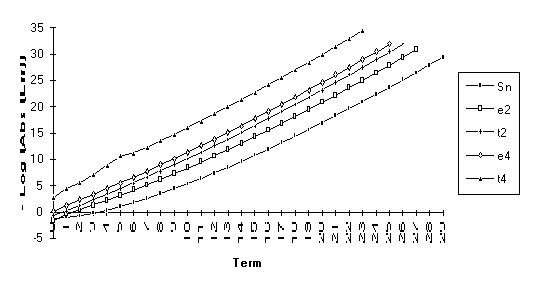
![]()
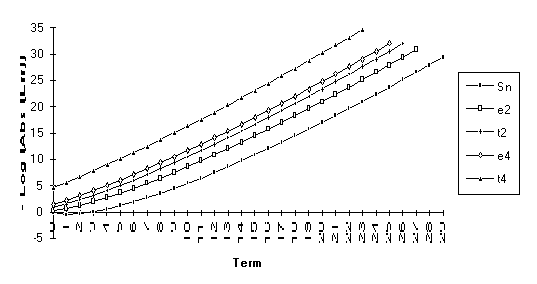
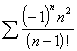
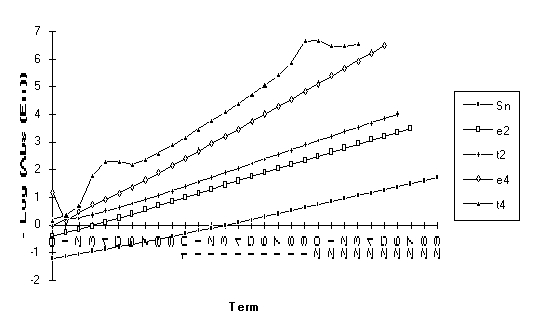
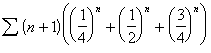
Note : The graphs of the transforms of this function have a significantly larger slope than the original series. This indicates a change in the exponential rate of convergence.
![]()
![]()
![]()

![]()
![]()
![]()
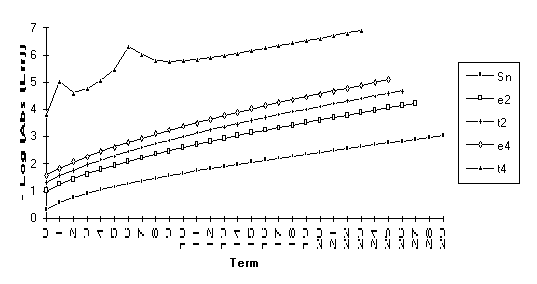
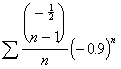
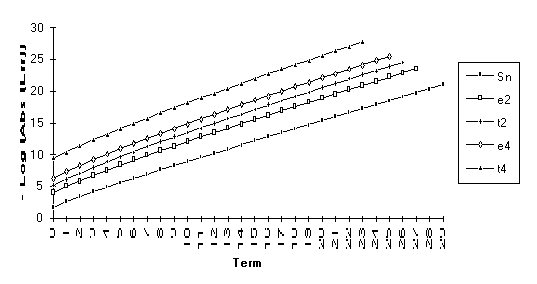
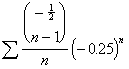
![]()
![]()
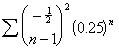
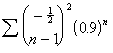
![]()
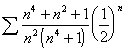
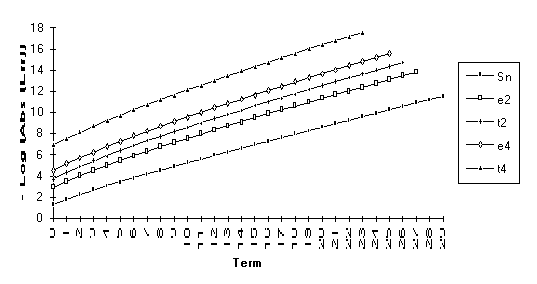
![]()
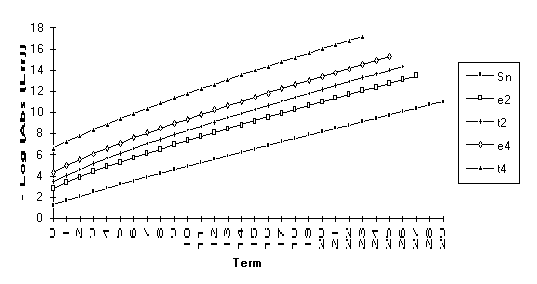

![]()
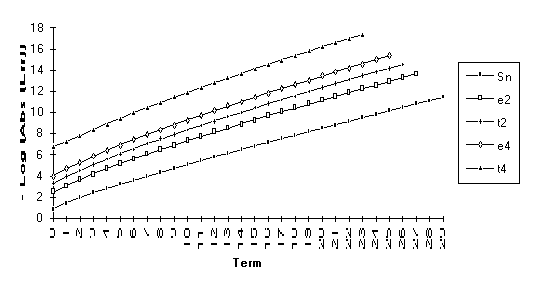
![]()
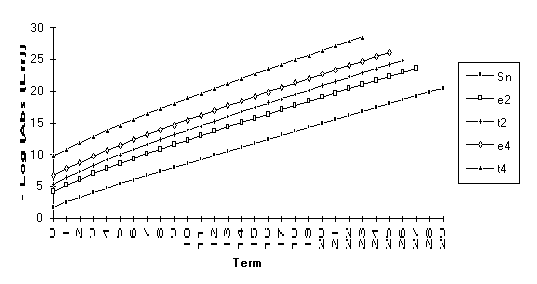
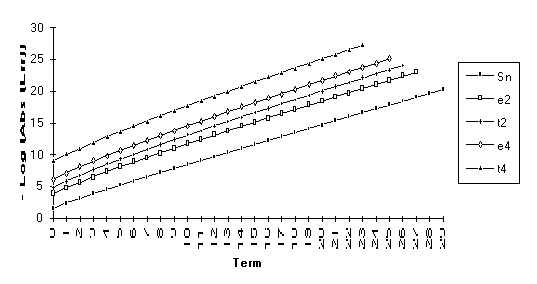
Group 2
This
group contains series for which ![]() is exact. These series can all be shown to be a
combination of a limit and two exponential transients. Notice that, for all of these series, the
order of performance (from best to worst) is
is exact. These series can all be shown to be a
combination of a limit and two exponential transients. Notice that, for all of these series, the
order of performance (from best to worst) is ![]() .
.
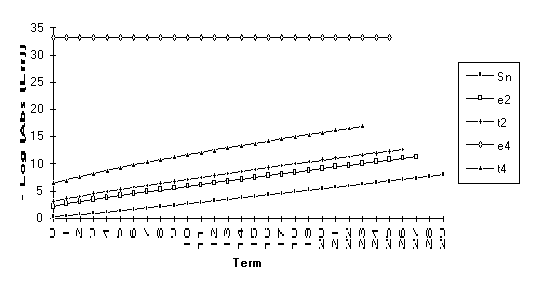
![]()
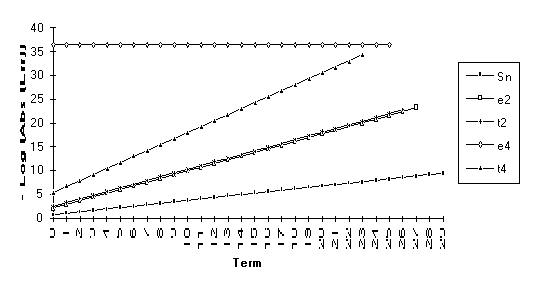
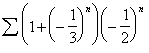
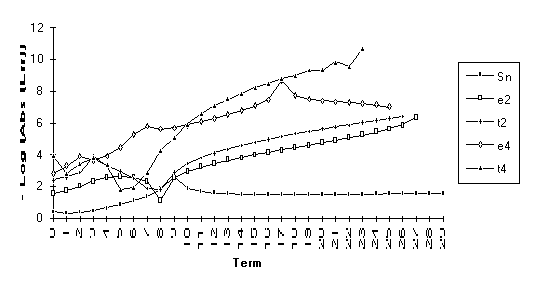
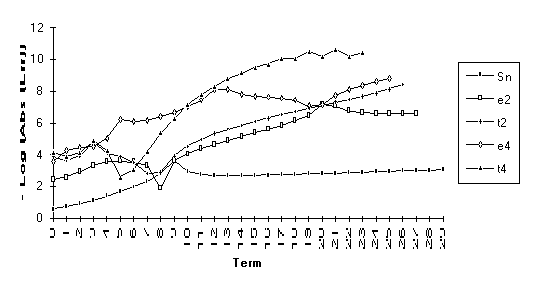
Group 3
This
group contains series for which ![]() eventually
outperforms
eventually
outperforms ![]() , but otherwise the results are unclear. All series in this group contain the
nonrational modifier
, but otherwise the results are unclear. All series in this group contain the
nonrational modifier ![]() .
.
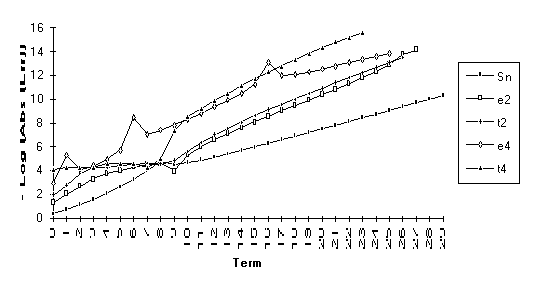
![]()
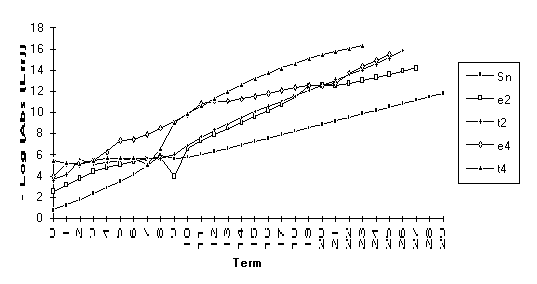
![]()

![]()
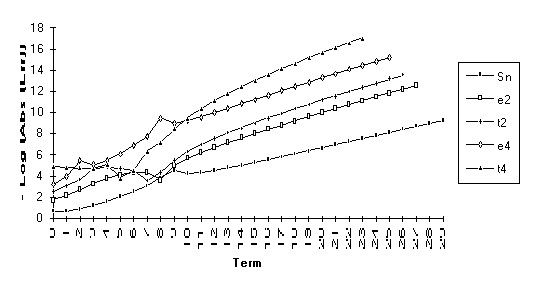
![]()
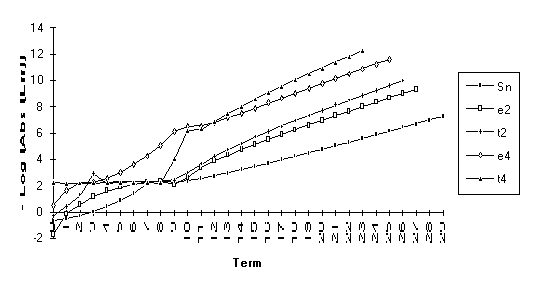
![]()
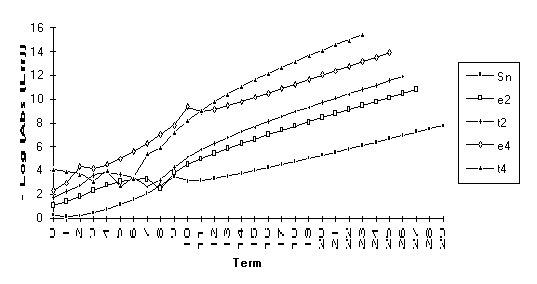
![]()
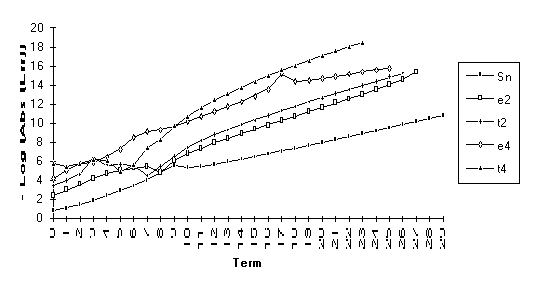
![]()
![]()

![]()
![]()

![]()
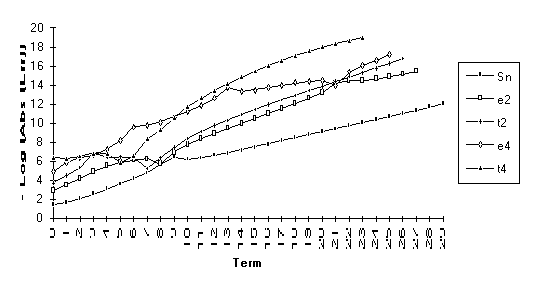
![]()
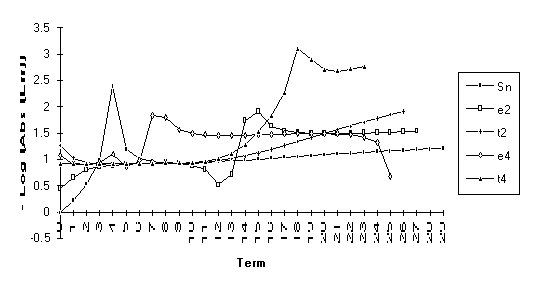
![]()
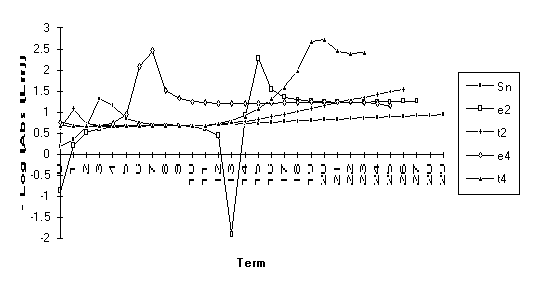
![]()
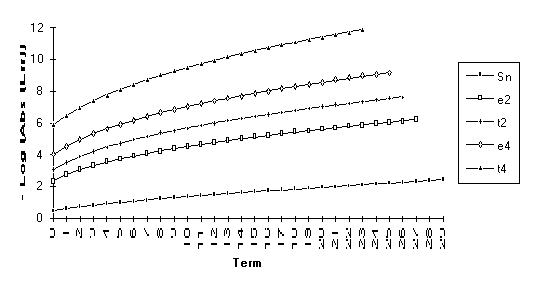
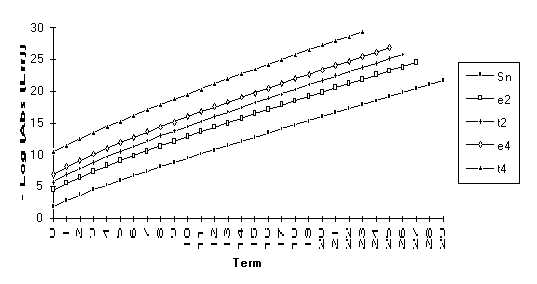
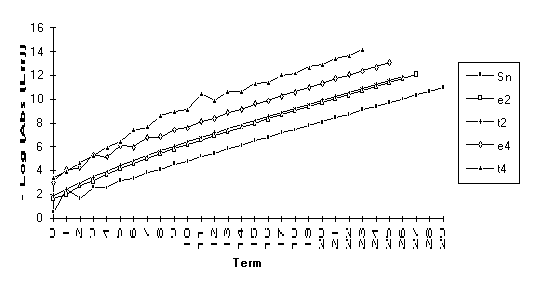
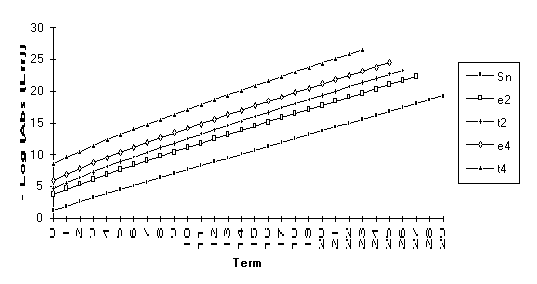
Group 4
This
group contains the series for which the following order of performance is
observed (from best to worst): ![]() . For all but the
first series in this group, the
. For all but the
first series in this group, the ![]() -algorithm will eventually be exact.
-algorithm will eventually be exact.

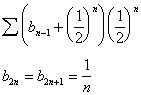
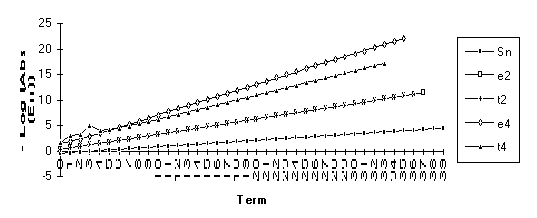
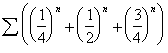
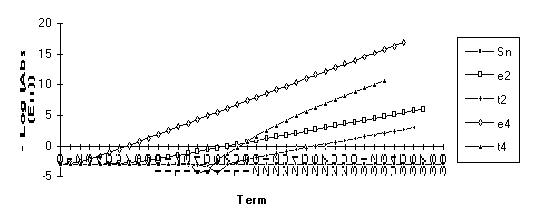
This sequence can be shown to be a combination of its limit and three exponential transients. The epsilon algorithm will then be exact by the sixth iteration. Notice here that the epsilon algorithm outperforms the theta algorithm. This is due to the fact that this is exactly the type of sequence that the e transform was designed to accelerate.

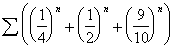
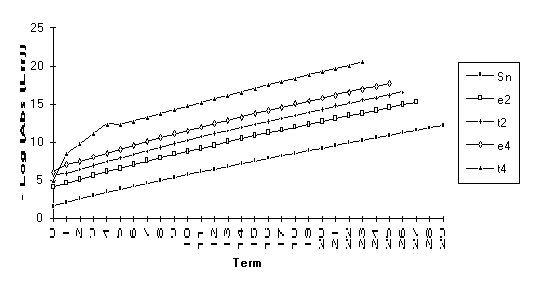
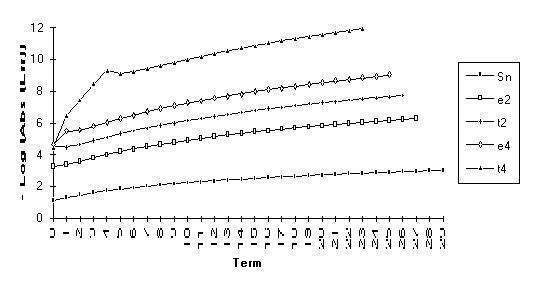
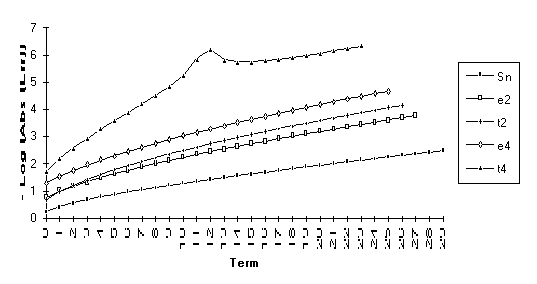
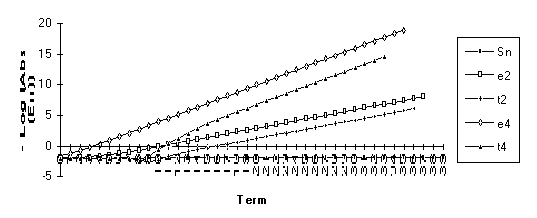
This and the next
three series are included to demonstrate the effect of singularities on the
transforms. All terms of both the ![]() -algorithm and the
-algorithm and the ![]() -algorithm are undefined at 1. The inclusion of the
successive terms 0.9, 0.99, and 0.999
illustrates the continuing degradation of the algorithms as the singularities
are approached.
-algorithm are undefined at 1. The inclusion of the
successive terms 0.9, 0.99, and 0.999
illustrates the continuing degradation of the algorithms as the singularities
are approached.
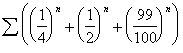
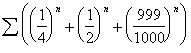
Group 5
This
group of series bears the following peculiar attribute: only ![]() achieves any
acceleration.
achieves any
acceleration.

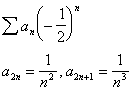
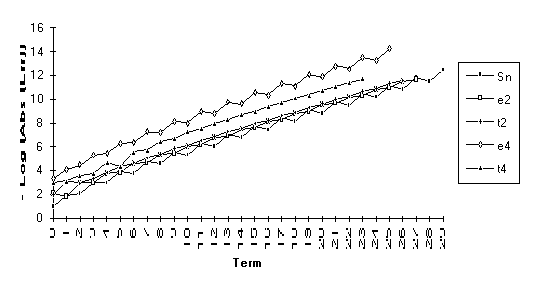
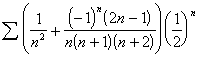
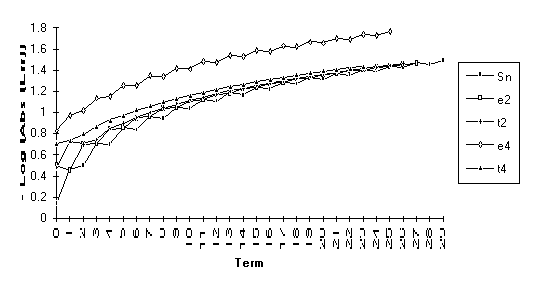
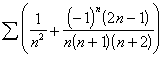
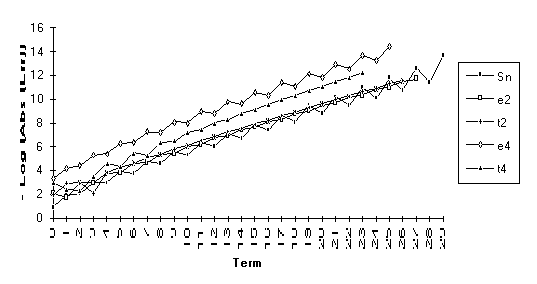
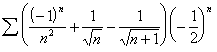
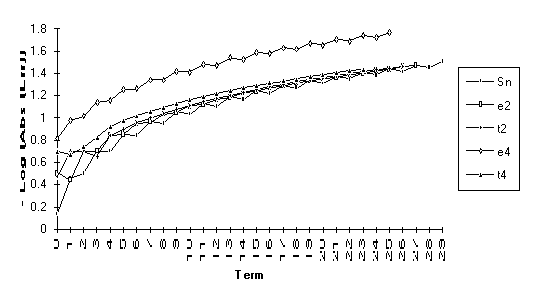
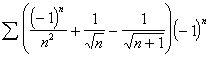
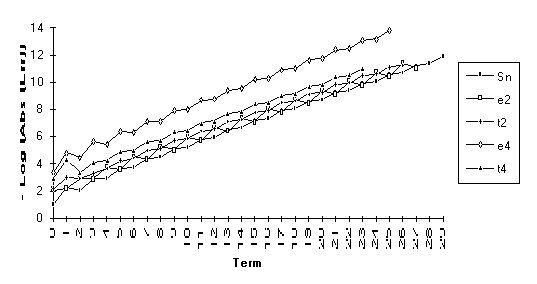
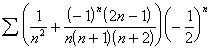
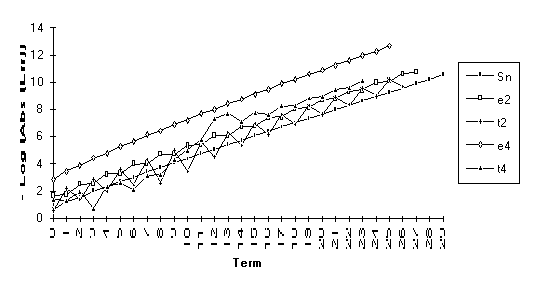
![]()
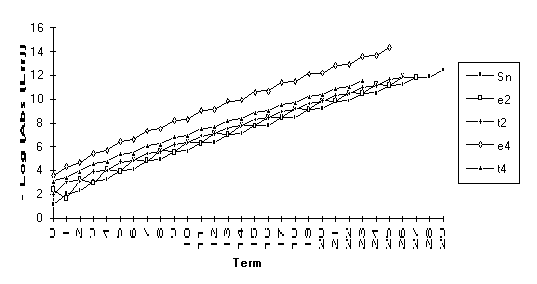

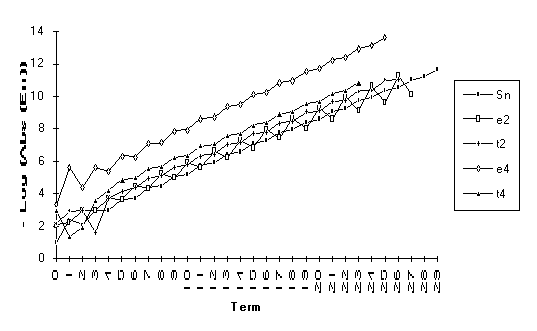
![]()
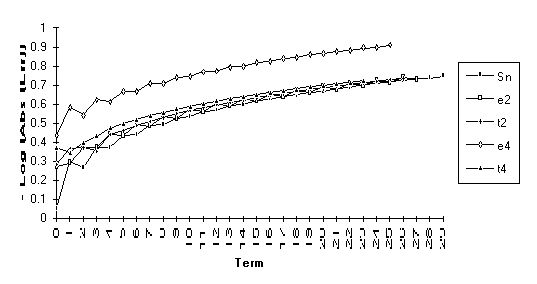
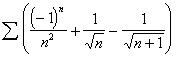
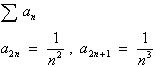
Note: For the above function, 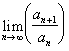 does not exist, but
does not exist, but 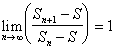 .
.
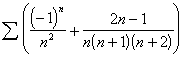
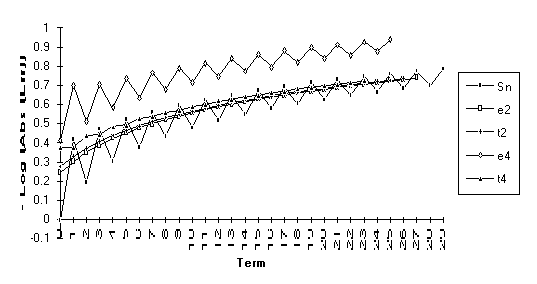
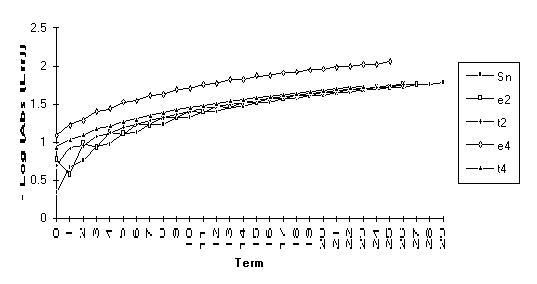
![]()
Note: For this series, 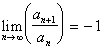 , but
, but 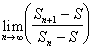 does not exist.
does not exist.
Group 6
This group consists of a single
series which none of the algorithms considered accelerated.
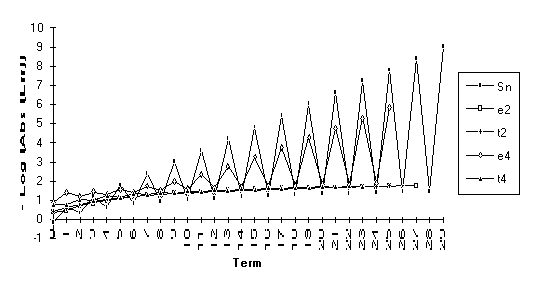
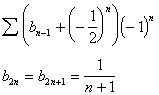
Note: For this series, 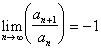 , but
, but  .
.
Group 7
For
this group of series, the following order of performance is observed (from best
to worst): ![]() .
.
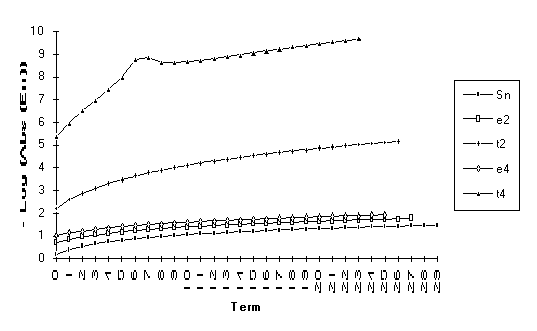
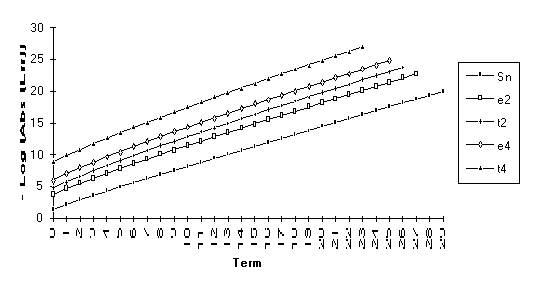
![]()
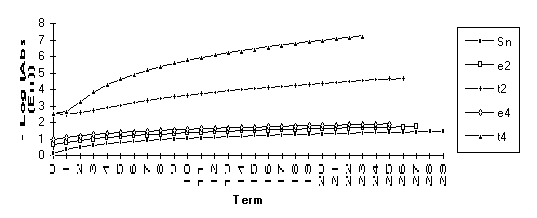
![]()
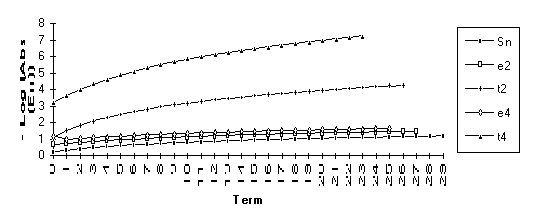
![]()
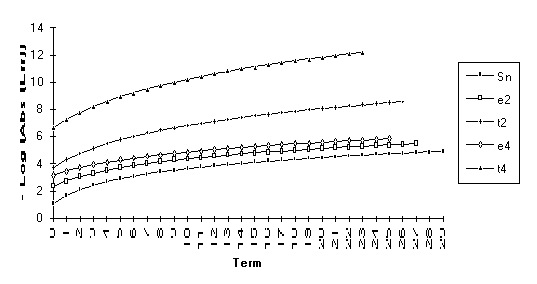
![]()
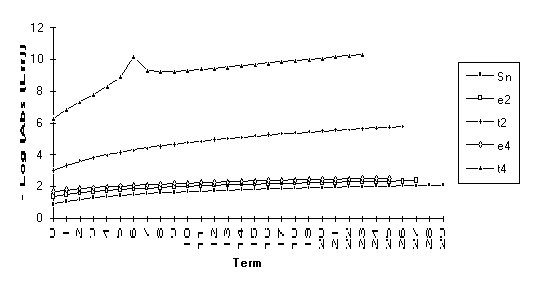
![]()

![]()
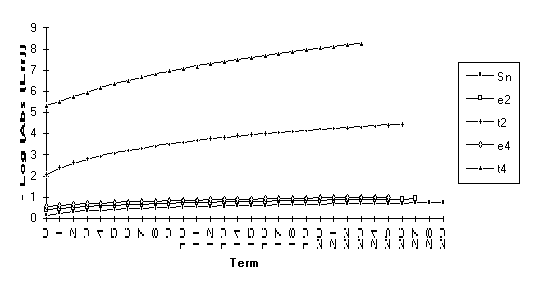
![]()
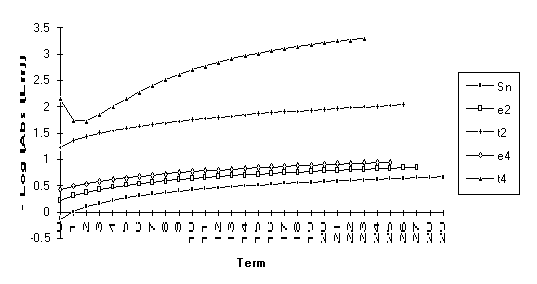
![]()
Section 4
Summary
Several conclusions have been reached in this paper; this section summarizes these results. The two lemmas presented in Section 3 are worthy of special mention here. In any practical application of the algorithms addressed in this paper, it is critical to be aware of any anomalies that might occur. The graphs associated with the lemmas illustrated the profound effect a singularity can have on a transform.
In
the series considered, ![]() outperformed
outperformed ![]() except for a few
cases.
except for a few
cases.
There
did not appear to be a change in the exponential rate of convergence between ![]() and
and ![]() unless otherwise
noted.
unless otherwise
noted.
No evidence of numeric instability was observed in any of the transforms considered (only in the case where a transform was nearly undefined could any instability be seen).
Bibliography
[1] Baker, George A., Jr.
Essentials of Padé Approximants
Academic Press, New York, 1975
[2] Brezinski, Claude.
Acceleration de suites a convergence logarithmique.
C. R. Acad. Sc. Paris, 18 October 1971, p. 727-730.
[3] Clark, W. D., Gray, H. L., Adams, J. E.
A Note on the T-Transformation of Lubkin.
Journal of Research of the National Bureau of Standards, B. Mathematical Sciences, Vol 73B, No. 1, January - March 1969, p. 25-29.
[4] Delahaye, Jean-Paul.
Sequence Transformations.
Springer-Verlag, 1980.
[5] Shanks, Daniel.
Non-Linear Transformations of Divergent and Slowly Convergent Sequences.
Journal of Mathematics and Physics, Vol 34, 1955, p. 1-42.
[6] Smith, David A., Ford, William F.
Acceleration of Linear and Logarithmic Convergence.
Journal of Numerical Analysis, Vol 10, No. 2, April 1979, p. 223-240.
[7] Smith, David A., Ford, William F.
Numerical Comparisons of Nonlinear Convergence Accelerators.
Mathematics of Computation, Vol. 38, No. 158, p. 481-499.
[8] Wimp, Jet.
Sequence Transformations and Their Applications.
Academic Press, 1981, p. 120-147.
[9] Wynn, P.
On a Device for Computing the em(Sn) Transformation.
Mathematical Aids to Computation, Vol. 10, 1956, p. 91-96.
[10] Wynn, P.
On the Convergence and Stability of the Epsilon Algorithm.
Siam Journal of Numerical Analysis, Vol. 3, No. 1, 1966, p. 91-122.